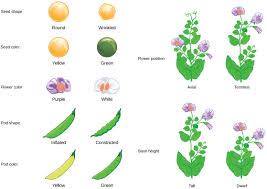
Gregor Mendel, recognized as the “father of genetics,” laid the foundation for modern genetics through his meticulous experiments with pea plants. His work introduced two fundamental principles: the Principle of Segregation and the Principle of Independent Assortment.
These principles are pivotal in understanding inheritance patterns in crops. The chi-square (χ²) statistical method is instrumental in predicting outcomes of various genetic crosses, including monohybrid, dihybrid, and trihybrid crosses.
Read Also: How to Grow, Use and Care for Wiegand’s Sedge Grass (Carex wiegandii)
Mendel’s Experiment and Its Significance in Crop Breeding
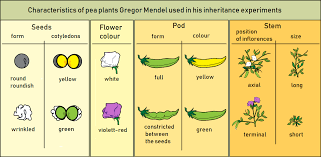
Mendel conducted a cross between tall and dwarf pea plants by transferring pollen from the dwarf plant to the stigma of the tall plant, resulting in F1 seeds.
Upon planting, all F1 plants exhibited tall phenotypes. Self-pollination of these F1 plants produced F2 seeds, which, when planted, yielded both tall and dwarf plants in a phenotypic ratio of 3:1. This observation marked a significant milestone in crop breeding.
Illustration of Mendel’s Cross:
- Parents: TT (Tall) × tt (Dwarf)
- Gametes: T and t
- F1 Generation: All Tt (Tall)
- F2 Generation: TT, Tt, Tt, tt
Summary of F2 Generation:
| Phenotype | Genotype | Genotypic Frequency | Phenotypic Ratio |
|---|---|---|---|
| Tall | TT | 1 | |
| Tall | Tt | 2 | 3 (1+2) |
| Dwarf | tt | 1 | 1 |
In the F2 generation, the genotypic ratio is 1:2:1, while the phenotypic ratio is 3:1, characteristic of monofactorial crosses.
Read Also: How to Grow, Use and Care for Whitetop Sedge Grass (Rhynchospora colorata)
Fundamental Principles of Inheritance in Agricultural Genetics
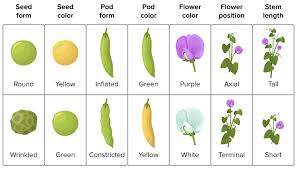
1. Principle of Segregation
This principle states that during gamete formation, the two alleles for a gene separate so that each gamete carries only one allele. For instance, a plant possessing alleles for both round and wrinkled seeds will transmit only one allele to its offspring.
2. Principle of Independent Assortment
According to this principle, alleles of different genes assort independently during gamete formation, provided the genes are located on different chromosomes.
Monohybrid Crosses in Agricultural Genetics
A monohybrid cross involves a single pair of contrasting traits. For example, seed color governed by alleles B (black) and b (white). The parental generation is denoted as P, and the first filial generation as F1.
Examples:
- P: BB (Black) × BB (Black) → F1: All BB (Black)
- P: BB (Black) × Bb (Black) → F1: BB and Bb (All Black)
- P: BB (Black) × bb (White) → F1: All Bb (Black)
- P: Bb (Black) × Bb (Black) → F1: BB, Bb, bb (Black and White)
- P: Bb (Black) × bb (White) → F1: Bb (Black), bb (White)
- P: bb (White) × bb (White) → F1: All bb (White)
Dihybrid Crosses and Their Application in Crop Improvement
Dihybrid crosses involve two genes with four alleles. For example, crossing a pea plant with yellow round seeds (AABB) with one having green wrinkled seeds (aabb) results in F1 offspring with genotype AaBb (yellow round). Selfing the F1 generation yields an F2 generation with a phenotypic ratio of 9:3:3:1.
Calculation of Gametes and Genotypes:
- Number of gametes: 2ⁿ (n = number of heterozygous loci)
- Number of genotypes: 3ⁿ
For AaBb (n=2):
- Gametes: 2² = 4
- Genotypes: 3² = 9
F2 Generation Punnett Square:
| AB | Ab | aB | ab | |
|---|---|---|---|---|
| AB | AABB | AABb | AaBB | AaBb |
| Ab | AABb | AAbb | AaBb | Aabb |
| aB | AaBB | AaBb | aaBB | aaBb |
| ab | AaBb | Aabb | aaBb | aabb |
Phenotypic Ratios:
- Yellow Round: 9
- Yellow Wrinkled: 3
- Green Round: 3
- Green Wrinkled: 1
Trihybrid Crosses in Advanced Plant Breeding
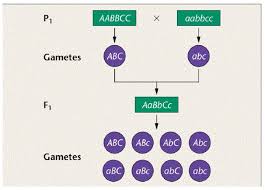
Trihybrid crosses involve three pairs of contrasting traits. Crossing AABBCC with aabbcc results in F1 offspring with genotype AaBbCc. The number of gametes produced is 2³ = 8, and the number of genotypes in the F2 generation is 3³ = 27.
Gametes from AaBbCc:
- ABC, ABc, AbC, Abc, aBC, aBc, abC, abc
Forked-Line Method:
This method simplifies the prediction of genotypic and phenotypic ratios in complex crosses by breaking down the cross into multiple monohybrid crosses.
General Rules:
| Number of Heterozygous Gene Pairs (n) | Number of Different Gametes (2ⁿ) | Number of Different F2 Genotypes (3ⁿ) | Number of Different F2 Phenotypes (2ⁿ) |
|---|---|---|---|
| 1 | 2 | 3 | 2 |
| 2 | 4 | 9 | 4 |
| 3 | 8 | 27 | 8 |
| 4 | 16 | 81 | 16 |
Example:
Crossing DdGgWw × DdGgWw:
- Number of gametes: 2³ = 8
- Number of genotypes: 3³ = 27
Application of Chi-Square (χ²) in Genetic Analysis
The chi-square test evaluates the goodness of fit between observed and expected data, crucial in determining inheritance patterns in crops.
Chi-Square Formula:
χ² = Σ[(O – E)² / E]
Where:
- O: Observed frequency
- E: Expected frequency
Example: Monohybrid Cross
Observed: 740 yellow, 260 white cotyledons
Expected (3:1 ratio): 750 yellow, 250 white
Calculations:
- Yellow: (740 – 750)² / 750 = 0.13
- White: (260 – 250)² / 250 = 0.4
Total χ²: 0.13 + 0.4 = 0.53
Degrees of Freedom (df): n – 1 = 2 – 1 = 1
Critical Value at 0.05 significance level: 3.84
Since 0.53 < 3.84, the observed data fits the expected ratio.
Example: Dihybrid Cross
Observed:
i. Yellow Round: 439
ii. Yellow Wrinkled: 168
iii. Green Round: 133
iv. Green Wrinkled: 60
Expected (9:3:3:1 ratio out of 800 plants):
i. Yellow Round: 450
ii. Yellow Wrinkled: 150
iii. Green Round: 150
iv. Green Wrinkled: 50
Calculations:
- Yellow Round: (439 – 450)² / 450 = 0.27
- Yellow Wrinkled: (168 – 150)² / 150 = 2.16
- Green Round: (133 – 150)² / 150 = 1.89
- Green Wrinkled: (60 – 50)² / 50 = 2.00
Total χ²: 0.27 + 2.16 + 1.89 + 2.00 = 6.32
Degrees of Freedom (df): 4 – 1 = 3
Critical Value at 0.05 significance level: 7.81
Since 6.32 < 7.81, the observed data fits the expected ratio, indicating independent assortment.
Mendel’s principles and the application of chi-square analysis are fundamental in agricultural genetics, aiding in the prediction and validation of inheritance patterns in crop breeding programs.
Do you have any questions, suggestions, or contributions? If so, please feel free to use the comment box below to share your thoughts. We also encourage you to kindly share this information with others who might benefit from it. Since we can’t reach everyone at once, we truly appreciate your help in spreading the word. Thank you so much for your support and for sharing!